Бакланова Е.В., Чуб Е.Д.
ЭКОНОМЕТРИЧЕСКИЙ АНАЛИЗ ВОЗБУЖДЕННЫХ ДЕЛ ОБ АДМИНИСТРАТИВНЫХ ПРАВОНАРУШЕНИЯХ В СФЕРЕ ТАМОЖЕННОГО КОНТРОЛЯ ПОСЛЕ ВЫПУСКА ТОВАРОВ
УДК 33/51-7
Е.В. Бакланова, студент экономического факультета
Ростовского филиала Российской таможенной академии
e-mail: elizavetabaclanova@yandex.ru
Е.Д. Чуб, студент экономического факультета
Ростовского филиала Российской таможенной академии
e-mail: katysha201360395@gmail.com
Научный руководитель – М.М. Цвиль, доцент кафедры информатики и информационных таможенных технологий, кандидат физико-математических наук, доцент
e-mail: tsvilmm@mail.ru
Аннотация. В работе проводится эконометрический анализ административных правонарушений в области осуществления таможенного контроля после выпуска товаров в регионе деятельности ФТС России. С целью прогнозирования строится мультипликативная модель ряда по квартальным данным с 1 квартала 2017 года по 2 квартал 2022 года. Уравнение тренда строится с помощью введения фиктивных переменных. В результате по полученной модели сделан прогноз.
Ключевые слова: объем административных правонарушений, эконометрическая модель, тренд, сезонная составляющая, фиктивные переменные, прогноз.
Эконометрическое моделирование – это процесс построения статистической модели, которую можно использовать для прогнозирования значения исследуемой переменной. Прогнозы, основанные на эконометрическом моделировании, могут быть использованы в различных отраслях экономики для ее развития. Стратегической целью таможенной службы Российской Федерации является повышение уровня экономической безопасности. Таможенные органы являются одним из главных инструментов, обеспечивающих защиту национальных интересов страны на международном уровне, осуществляя контроль за перемещением товаров через таможенную границу в соответствии с законодательством РФ.
Главное управление таможенного контроля после выпуска товаров выполняет ряд функций, возложенных на него ФТС России, среди которых выявление и сокращение административных правонарушений в части своей компетенции в соответствии с законодательством РФ, а также участие в планировании деятельности ФТС России по вопросам, входящим в компетенцию Главного управления[4].
При помощи таможенного контроля таможенные органы выявляют правонарушения и преступления, как административные, так и уголовные, в области таможенного делана стадии после выпуска товаров до того времени, пока не истечет три года. В нашей работе мы сделаем акцент именно на административных правонарушениях. Цель данной работы провести эконометрический анализ возбужденных дел об АП в сфере таможенного контроля после выпуска товаров.
Для достижения поставленной цели, разработаем эконометрическую модель для последующего прогнозирования количества выявленных дел об АП в области таможенного дела. Тематика статьи достаточно актуальна на современном этапе развития экономики таможенного дела.
Данные для построения эконометрической модели по количеству возбужденных дел об АП в области осуществления таможенного контроля после выпуска товаров были взяты с официального сайта Федеральной таможенной службы и представлены в табл.1.
Таблица 1
Количество возбужденных дел об АП в сфере осуществления таможенного контроля после выпуска товаров, шт.
| Период | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| I | 1399 | 1548 | 1345 | 1860 | 1 935 | 1952 |
| II | 1107 | 1319 | 1104 | 1859 | 1528 | 1482 |
| III | 1171 | 1259 | 1335 | 1754 | 1624 | — |
| IV | 1547 | 1542 | 1543 | 1827 | 2447 | — |
Источник: составлена авторами на основе [4].
Моделирование целесообразно начать с построения графика. Таким образом, данные из табл. 1 следует представить в виде временного ряда, рис.1. Стоит отметить, что yt мы рассматриваем по кварталам, а значит и прогнозное значение в дальнейшем будем определять за третий и четвертый кварталы 2022 года.
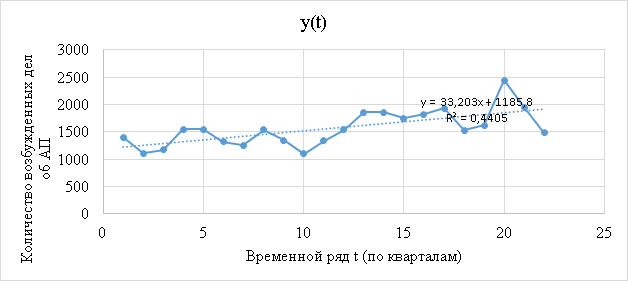
Рис. 1. Графическая интерпретация количества возбужденных дел об АП в сфере осуществления таможенного контроля после выпуска товаров, шт.
Источник: разработан авторами на основе [2–3].
Опираясь на полученный график, мы можем сделать вывод, что временной ряд имеет сезонную составляющую с период l=4 и возрастающий линейный тренд. Исходя из этого, мы будем строить мультипликативную модель временного ряда, представленную формулой (1): Y=T x S x E, (1)
где Т – трендовая,
S – сезонная,
Е – случайная компонента[3].
Выравнивая ряд, при помощи метода усреднения, так называемого, скользящей средней, мы рассчитали оценки сезонных составляющих и полученные значения представили в табл.2.
Таблица 2
Применение метода скользящей средней для выравнивания ряда, расчет оценки сезонной компоненты
| Год | t | y(t) | Скользящая ср. за 4 квартала | Центрированная ср. за 4 квартала | Оценка сезонности S | S(t) |
| 2017 | 1 | 1399 | — | — | — | 1,074 |
| 2 | 1107 | — | — | — | 0,906 | |
| 3 | 1171 | 1306,000 | 1324,625 | 0,884 | 0,908 | |
| 4 | 1547 | 1343,250 | 1369,750 | 1,129 | 1,112 | |
| 2018 | 5 | 1548 | 1396,250 | 1407,250 | 1,100 | 1,074 |
| 6 | 1319 | 1418,250 | 1417,625 | 0,930 | 0,906 | |
| 7 | 1259 | 1417,000 | 1391,625 | 0,905 | 0,908 | |
| 8 | 1542 | 1366,250 | 1339,375 | 1,151 | 1,112 | |
| 2019 | 9 | 1345 | 1312,500 | 1322,000 | 1,017 | 1,074 |
| 10 | 1104 | 1331,500 | 1331,625 | 0,829 | 0,906 | |
| 11 | 1335 | 1331,750 | 1396,125 | 0,956 | 0,908 | |
| 12 | 1543 | 1460,500 | 1554,875 | 0,992 | 1,112 | |
| 2020 | 13 | 1860 | 1649,250 | 1701,625 | 1,093 | 1,074 |
| 14 | 1859 | 1754,000 | 1789,500 | 1,039 | 0,906 | |
| 15 | 1754 | 1825,000 | 1834,375 | 0,956 | 0,908 | |
| 16 | 1827 | 1843,750 | 1802,375 | 1,014 | 1,112 | |
| 2021 | 17 | 1935 | 1761,000 | 1744,750 | 1,109 | 1,074 |
| 18 | 1528 | 1728,500 | 1806,000 | 0,846 | 0,906 | |
| 19 | 1624 | 1883,500 | 1885,625 | 0,861 | 0,908 | |
| 20 | 2447 | 1887,750 | 1882,000 | 1,300 | 1,112 | |
| 2022 | 21 | 1952 | 1876,250 | — | — | 1,074 |
| 22 | 1482 | — | — | — | 0,906 |
Источник: разработана авторами на основе [4].
Для того, чтобы произвести корректировку сезонной составляющей, мы использовали полученные данные из табл.2. Таким образом, для начала, были рассчитаны за каждый год рассматриваемого периода (2017–2022) суммы оценок сезонной составляющей по кварталам. Затем, важным этапом было нахождение их средних значений, также рассчитанных по каждому кварталу рассматриваемого периода, сумма которых должна быть приближена к количеству период в временном ряде (в нашем случае l=4). Этот этап является важным так как на его основе мы находим коэффициент, который потребуется нам для корректировки оценок сезонных составляющих. Значение коэффициента мы находим при помощи деления количества периодов на сумму средних оценок сезонных. Полученный коэффициент умножаем поквартально на средние значения оценок сезонных компонентов. Результаты произведенных расчетов считаются верными, если сумма скорректированных значений будет принимать значение равное периодам сезонной составляющей l, рис. 2.
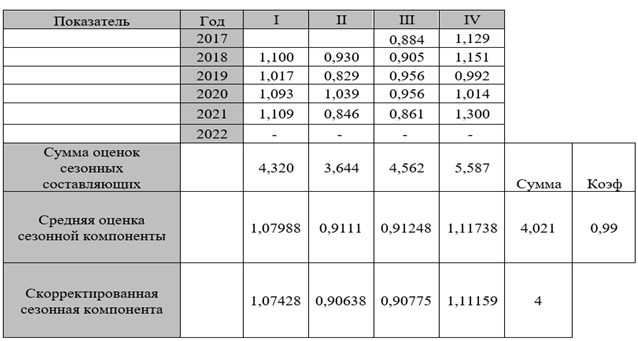
Рис. 2. Скорректированные значения сезонной компоненты
Источник: разработан авторами на основе [2–3].
Следующим шагом, мы разделили фактические значения временного ряда y(t) на соответствующие скорректированные сезонные составляющие S(t) и на основе полученных данных построили график, представленный на рис.3.
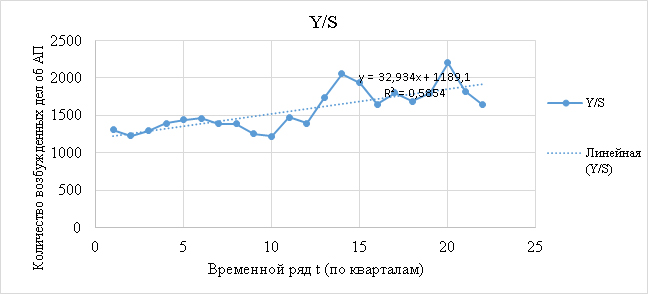
Рис. 3. Линейный тренд, построенный на основе скорректированных данных
Источник: разработан авторами на основе [1].
Проведем статистический анализ модели y=1189,085+32,934t при помощи инструментов Excel «Анализ данных» → «Регрессия», рис. 4.
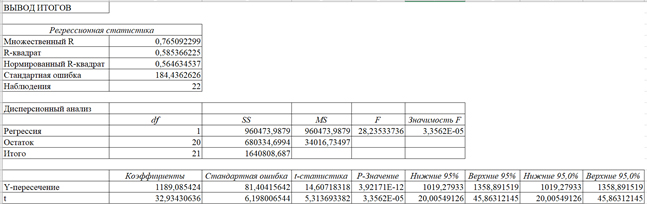
Рис. 4. Регрессионный анализ на основе Y/S
Источник: разработан авторами на основе [2–3].
Для того, чтобы сделать выводы по модели y=1189,085+32,934tстоит рассмотреть полученные значения регрессионного анализа. Для начала обратим внимание на t-статистики, как показывает анализ, они являются значимыми, так как превышают табличное значение. Далее стоит обратить внимание на фактическое значение F-критерия Фишера, в нашем случае оно равно 28,235, соответственно также, как и t-статистики принимает значение больше табличного. Но также одним из важных показателей является коэффициент детерминации, который должен принимать высокие значения приближенные к единице, однако, если мы обратим внимание на значения R2 по нашей модели мы сможем прийти к выводу, что рассматриваемая модель не подходит для прогноза так как коэффициент детерминации равен 0,585. Для того, чтобы убедиться в нашем предположении мы вычислим долю ошибки прогноза в процентном формате по формуле (2):
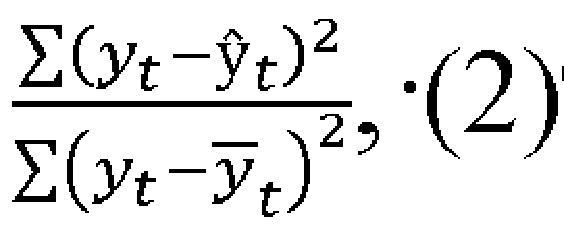
где ŷt расчетные значения линейного тренда по модели y=1189,085+32,934t,
ȳt − среднее арифметическое фактических значений временного ряда.
Произведя необходимые расчеты, мы получили долю ошибки равную 30%. Наше предположение о незначимости полученной модели подтвердилось, следовательно, производить прогноз по модели y=1189,085+32,934t нельзя, так как полученные значения не будут отображать реальные показатели в будущем.
В процессе выполнения работы было определено, что при эконометрическом моделировании временного ряда есть смысл введения фиктивных переменных для того, чтобы значительно улучшить прогнозные показатели. Как известно, фиктивная переменная может принимать только лишь пару значений – единицу и ноль, в связи с чем происходит описание качественной характеристики, другими словами, фиктивная переменная показывает отклонения в рядах динамики от линии тренда.
Для этого мы вернемся к рис. 2 и отметим в каких кварталах имеются отклонения от линейного тренда. Данные всплески нам помогут сгладить введенные фиктивные переменные. После неоднократных подборов фиктивных переменных, мы пришли к окончательному уравнению тренда с такими показателями, как Z9, Z10, Z12, Z14, Z15, Z20, Z22, принимающих единицу для необходимого периода tи ноль для остальных, формула (3).
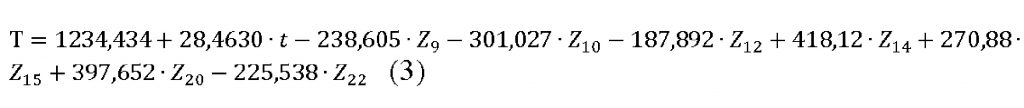
Произведем для улучшенной модели такой же статистический анализ, как и для прошлой (непригодной) модели, рис. 5.
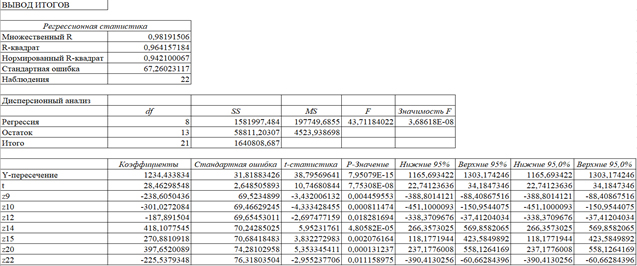
Рис. 5. Регрессионный анализ на основе уравнения тренда с применением фиктивных переменных
Источник: разработан авторами на основе [2–3].
В первую очередь рассмотрим те показатели, которые были благоприятными и в прошлой модели – t-статистики и F-критерий Фишера. Из рис. 5. мы видим, что t-статистики модели (3) являются также значимыми, так как принимают значения больше табличного и F-критерий Фишера, в свою очередь, тоже больше табличного значения и равняется 43,712. Отметим, что два данных показателя с введением фиктивных переменных не ухудшились, а только возросли, что имеет место в улучшении модели. Следующим шагом рассмотри показатели, которые в прошлой модели нас не удовлетворили – коэффициент детерминации и доля ошибки прогнозирования. Что и требовалось доказать, коэффициент детерминации при введении фиктивных переменных вырос более чем в 1,5 раза и на данном этапе R2=0,964, что соответственно имеет приближенное значение к единице. Также на основе формулы (2) мы рассчитали долю ошибки прогноза, после введения фиктивных переменных, и можем сделать вывод, что ошибка уменьшилась в 10 раз и приняла значение равное 3%, следовательно, данное значение является допустимым для таможенных органов и результаты прогноза можно считать максимально приближенными к реальности.
В результате мы получили мультипликативную модель для прогноза, где трендовая задана формулой (3), а значения сезонной берутся из табл.2.
Обязательным этапом является построение графика, на котором будет представлено соотношение фактических данных и рассчитанных по улучшенной модели с применением фиктивных переменных, рис. 6.
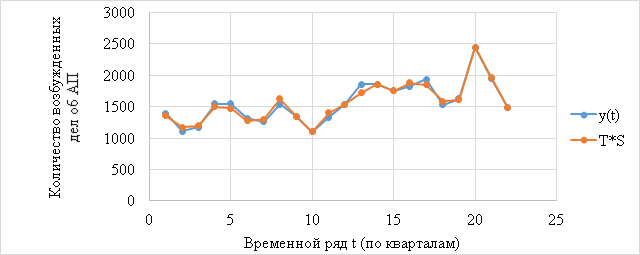
Рис. 6. Фактические данные и рассчитанные по улучшенной модели с применением фиктивных переменных
Источник: разработан авторами на основе [2–3].
Так как мы получили значимую модель при помощи введения фиктивных переменных нам следует сделать по ней прогноз на 3 и 4 квартал 2022 г. по количеству возбужденных дел об АП в сфере таможенного контроля после выпуска товаров, с учетом значения сезонной компоненты (S3=0,908; S4=1,112 соответственно). Для этого подставим в уравнение тренда (3) значение t=23;24. Получим 1836,07 и 2280,03 дел об АП в 3 и 4 кварталах соответственно.
Таким образом, подводя итоги проделанной работы, мы можем сделать вывод, что методика прогнозирования на основе введения фиктивных переменных является перспективной и имеет преимущество в виде простоты реализации.
Использованные источники:
- Кремер Н.Ш. Эконометрика: учебник для студентов вузов / Н.Ш. Кремер, Б.А. Путко; под ред. Н.Ш. Кремера. 3-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2012. 328 с.
- Цвиль М. М. Анализ временных рядов и прогнозирование: учеб. пособие. Ростов н/Д: Российская таможенная академия, Ростовский филиал, 2016. 135 с.
- Цвиль М. М. Эконометрика: конспекты лекций по учебной дисциплине. Ростов н/Д: Российская таможенная академия, Ростовский филиал, 2012. 86 с.
- Официальный сайт Федеральной таможенной службы [Электронный ресурс]. URL: https://customs.gov.ru
